IRT: Analysis of Test Items

IRT (Item Response Theory) is a family of statistical models used to analyze data from tests, questionnaires, and surveys, where each individual item (question) matters.

Unlike classical test theory, which focuses mainly on the total score (sum of points across items), IRT models the probability of a specific response to a specific item as a function of:

• properties of the item, and
• characteristics (ability or trait level) of the respondent.

The key components of IRT are:

• Item difficulty (b) – how "hard" the item is; items with higher b are more difficult.
• Item discrimination (a) – how well the item distinguishes between respondents with different levels of the trait (e.g., math ability, anxiety).
• Guessing probability (c) – in some models, the lower asymptote that captures the chance of getting an item right by guessing (typical for multiple-choice questions).
• Respondent ability (θ) – the underlying trait or ability being measured (e.g., language proficiency, depression severity).

IRT is widely used in:

• education (exams, placement tests, computerized adaptive testing),
• psychology and clinical assessment (scales for depression, anxiety, etc.),
• social and market research (attitude scales, Likert Scale based instruments, etc.),
• UX and CX measurement (under the hood of some CSI, ACSI or UEQ-style scales).

IRT allows you to:

• understand how each item behaves,
• build adaptive tests,
• equate different test forms,
• and track changes in abilities or traits over time (e.g., in longitudinal studies).

What is the purpose of IRT assessment?

IRT-based assessment is used wherever tests or scales need to be reliable, comparable and fair. Key applications include:

1. Test development and analysis

IRT helps test designers:

• assess item quality (difficulty, discrimination, guessing),
• remove or revise poorly performing items,
• ensure that a test measures the intended construct consistently.

Compared to just looking at raw percentages or total scores, IRT-based analysis provides much richer insight into how each item works across different ability levels. This is crucial when building high-stakes assessments or standardized scales (educational tests, employee engagement surveys, clinical instruments, etc.).

2. Adaptive testing (CAT)

One of the most famous uses of IRT is Computerized Adaptive Testing (CAT):

• The test starts with items of medium difficulty.
• Based on the respondent's answers, the system estimates their ability (θ).
• The next items are chosen dynamically to be more informative for that estimated level.

This gives:

• more accurate measurement,
• with fewer items,
• and reduced test time and fatigue.

Many large-scale exams and online assessment platforms rely on IRT-based CAT to deliver efficient, individualized testing.

3. Evaluation and comparison of items and tests

Because IRT places both items and respondents on the same latent scale (θ), it enables:

• comparison of items across different test forms,
• test equating (ensuring scores from different versions are comparable),
• evaluation of how items behave in different panels, cohorts or cultures.

This is especially useful for longitudinal programs, regular certification exams, or multi-language test versions where fairness and comparability matter.

4. Research and development of educational programs

In education and training, IRT helps:

• analyze patterns of correct/incorrect responses,
• identify content areas where learners systematically struggle,
• refine curricula and teaching strategies based on item-level insight.

When combined with experimental research and time series analysis, IRT supports rigorous evaluation of program effectiveness.

5. Cross-cultural and multilingual assessment

IRT is powerful in cross-cultural research:

• the same test can be administered in different languages,
• item parameters can be tested for invariance (does the item behave similarly across groups?),
• problematic items (biased or culture-specific) can be detected and revised.

This helps ensure fair testing and comparable scores across countries or demographic groups, and often goes hand-in-hand with Delphi Method expert reviews or cognitive interviewing.

6. Diagnostics and clinical assessment

In medicine and psychology, IRT supports:

• building robust diagnostic scales (e.g., depression, anxiety, quality of life),
• customizing assessments (short forms, adaptive versions),
• tracking patient progress over time with more precision.

Here, IRT-based instruments can be paired with VAS, Likert scales, and other measurement tools, and analyzed alongside metrics like CSI or ACSI in patient experience work.

7. Social and psychological research

In social sciences and market research, IRT is used to analyze:

• attitudes and opinions,
• personality traits,
• behavior scales (e.g., engagement, satisfaction, burnout through tools like MBI).

It complements factor analysis and qualitative analysis, and can be integrated into large panel or cross-sectional surveys to improve measurement quality.

How is the IRT metric calculated?

In IRT, there is not "one metric" but rather a model that describes the relationship between:

• item parameters (a, b, c), and
• respondent ability (θ),

and the probability of a given response (usually a correct answer or endorsement). Different IRT models are used depending on the situation.

1. Choosing an IRT model

The most common models for dichotomous (right/wrong) items are:

• 1PL (Rasch model). Assumes all items have the same discrimination; only item difficulty (b) and ability (θ) are estimated.
• 2PL model. Estimates both difficulty (b) and discrimination (a) for each item, allowing some items to be more informative than others.
• 3PL model. Adds the guessing parameter (c), which represents the probability of getting the item correct purely by guessing (especially for multiple-choice items).

For rating scales (e.g., Likert items), there are polytomous IRT models, such as the graded response model or partial credit model, which extend the same principles.

2. Estimating item parameters

Given a dataset of respondents' answers:

• IRT uses algorithms (often maximum likelihood estimation or Bayesian methods) to estimate a, b, c for each item.
• These estimates express how likely respondents at different ability levels are to respond correctly (or endorse a category).

This process usually requires specialized software and is often combined with factor analysis steps to ensure the scale measures a single dominant trait.

3. Estimating respondent abilities (θ)

Once item parameters are known, the next step is to estimate each respondent's ability (θ):

• For each respondent, the estimation method finds the θ value that maximizes the likelihood of their observed pattern of responses.
• In adaptive testing, θ is updated after each new item answer, and the next item is chosen to be most informative for the current estimate.

These θ values can be transformed to more familiar scales (e.g., mean 0 and SD 1, or 100-point scales), or linked to external metrics such as proficiency levels.

4. Model formulas

For the 2PL model, the probability P(θ) that a respondent with ability θ answers an item correctly (with parameters a and b) is:

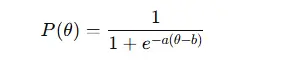
For the 3PL model, which includes guessing (c):

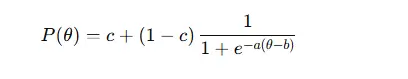
• a – item discrimination
• b – item difficulty
• c – guessing parameter
• θ – respondent ability

These functions generate item characteristic curves (ICCs) that show how the probability of a correct answer changes with ability.

5. Example (2PL model)

Consider a 2PL item with:

• difficulty b=−1b = -1b=−1,
• discrimination a=1.5a = 1.5a=1.5,
• and a respondent with ability θ=0.5.

The probability of a correct answer is:

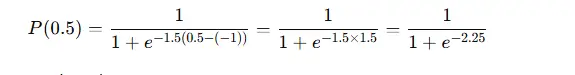
Numerically, this is approximately:

P(0.5) ≈ 0.905 (90.5%)

So for a respondent at this ability level, the item is relatively easy.

6. Using IRT outputs

After estimating item and person parameters, you can:

• remove or revise bad items (low discrimination, strange ICCs),
• design short forms that retain most of the information,
• build adaptive tests,
• compare scores across different versions of a test,
• evaluate changes in ability over time (e.g., pre-/post-training in experimental research).

IRT-based scales can also be connected to other metrics in your measurement system-like CSI, ACSI, Employee Engagement, or UEQ-to create more robust, scientifically grounded instruments.

In practice, implementing IRT involves complex statistical methods and dedicated software, but the payoff is significant: tests and questionnaires become more precise, more fair, and more comparable, especially when used repeatedly or across different groups.