IRT: Análisis de Ítems de Prueba

La IRT (Teoría de Respuesta al Ítem) es una familia de modelos estadísticos utilizados para analizar datos de pruebas, cuestionarios y encuestas, donde cada ítem (pregunta) individual es importante.

A diferencia de la teoría clásica de pruebas, que se centra principalmente en el puntaje total (suma de puntos a través de los ítems), la IRT modela la probabilidad de una respuesta específica a un ítem específico como una función de:

• las propiedades del ítem, y
• las características (nivel de habilidad o rasgo) del encuestado.

Los componentes clave de la IRT son:

• Dificultad del ítem (b) – cuán "difícil" es el ítem; los ítems con un b más alto son más difíciles.
• Discriminación del ítem (a) – cuán bien el ítem distingue entre encuestados con diferentes niveles del rasgo (por ejemplo, habilidad matemática, ansiedad).
• Probabilidad de adivinanza (c) – en algunos modelos, el asintota inferior que captura la probabilidad de responder correctamente a un ítem por adivinanza (típico en preguntas de opción múltiple).
• Habilidad del encuestado (θ) – el rasgo o habilidad subyacente que se mide (por ejemplo, competencia lingüística, gravedad de la depresión).

La IRT se utiliza ampliamente en:

• educación (exámenes, pruebas de ubicación, pruebas adaptativas computarizadas),
• psicología y evaluación clínica (escalas para depresión, ansiedad, etc.),
• investigación social y de mercado (escalas de actitud, instrumentos basados en la Escala de Likert, etc.),
• medición de UX y CX (bajo el capó de algunos CSI, escalas al estilo ACSI o UEQ).

La IRT te permite:

• entender cómo se comporta cada ítem,
• construir pruebas adaptativas,
• equiparar diferentes formas de prueba,
• y rastrear cambios en habilidades o rasgos a lo largo del tiempo (por ejemplo, en estudios longitudinales).

¿Cuál es el propósito de la evaluación basada en IRT?

La evaluación basada en IRT se utiliza donde sea necesario que las pruebas o escalas sean confiables, comparables y justas. Las aplicaciones clave incluyen:

1. Desarrollo y análisis de pruebas

La IRT ayuda a los diseñadores de pruebas:

• a evaluar la calidad del ítem (dificultad, discriminación, adivinanza),
• a eliminar o revisar ítems de bajo rendimiento,
• a asegurar que una prueba mida el constructo deseado de manera consistente.

En comparación con simplemente observar porcentajes brutos o puntajes totales, el análisis basado en IRT proporciona una visión mucho más rica sobre cómo funciona cada ítem a través de diferentes niveles de habilidad. Esto es crucial al construir evaluaciones de alta importancia o escalas estandarizadas (pruebas educativas, encuestas de compromiso de empleados, instrumentos clínicos, etc.).

2. Pruebas adaptativas (CAT)

Uno de los usos más famosos de la IRT es la Prueba Adaptativa Computarizada (CAT):

• La prueba comienza con ítems de dificultad media.
• Basado en las respuestas del encuestado, el sistema estima su habilidad (θ).
• Los siguientes ítems se eligen dinámicamente para ser más informativos para ese nivel estimado.

Esto proporciona:

• una medición más precisa,
• con menos ítems,
• y reduce el tiempo de prueba y la fatiga.

Muchos exámenes a gran escala y plataformas de evaluación en línea dependen de la CAT basada en IRT para ofrecer pruebas eficientes e individualizadas.

3. Evaluación y comparación de ítems y pruebas

Debido a que la IRT coloca tanto ítems como encuestados en la misma escala latente (θ), permite:

• la comparación de ítems a través de diferentes formas de prueba,
• la equiparación de pruebas (asegurando que los puntajes de diferentes versiones sean comparables),
• la evaluación de cómo se comportan los ítems en diferentes paneles, cohortes o culturas.

Esto es especialmente útil para programas longitudinales, exámenes de certificación regulares o versiones de pruebas multilingües donde la equidad y la comparabilidad son importantes.

4. Investigación y desarrollo de programas educativos

En educación y formación, la IRT ayuda a:

• analizar patrones de respuestas correctas/incorrectas,
• identificar áreas de contenido donde los aprendices tienen dificultades sistemáticas,
• refinar planes de estudio y estrategias de enseñanza basadas en la información a nivel de ítem.

Cuando se combina con investigación experimental y análisis de series temporales, la IRT apoya la evaluación rigurosa de la efectividad del programa.

5. Evaluación transcultural y multilingüe

La IRT es poderosa en la investigación transcultural:

• la misma prueba se puede administrar en diferentes idiomas,
• los parámetros del ítem pueden ser probados para invarianza (¿se comporta el ítem de manera similar entre grupos?),
• se pueden detectar y revisar ítems problemáticos (sesgados o específicos de la cultura).

Esto ayuda a asegurar pruebas justas y puntajes comparables entre países o grupos demográficos, y a menudo va de la mano con revisiones de expertos del Método Delphi o entrevistas cognitivas.

6. Diagnósticos y evaluación clínica

En medicina y psicología, la IRT apoya:

• la construcción de escalas diagnósticas robustas (por ejemplo, depresión, ansiedad, calidad de vida),
• la personalización de evaluaciones (formas cortas, versiones adaptativas),
• el seguimiento del progreso del paciente a lo largo del tiempo con mayor precisión.

Aquí, los instrumentos basados en IRT pueden combinarse con VAS, escalas de Likert y otras herramientas de medición, y analizarse junto a métricas como CSI o ACSI en el trabajo de experiencia del paciente.

7. Investigación social y psicológica

En ciencias sociales e investigación de mercado, la IRT se utiliza para analizar:

• actitudes y opiniones,
• rasgos de personalidad,
• escalas de comportamiento (por ejemplo, compromiso, satisfacción, agotamiento a través de herramientas como MBI).

Complementa el análisis factorial y el análisis cualitativo, y puede integrarse en grandes paneles o encuestas transversales para mejorar la calidad de la medición.

¿Cómo se calcula la métrica de IRT?

En la IRT, no hay "una métrica" sino más bien un modelo que describe la relación entre:

• parámetros del ítem (a, b, c), y
• habilidad del encuestado (θ),

y la probabilidad de una respuesta dada (generalmente una respuesta correcta o aprobación). Se utilizan diferentes modelos de IRT dependiendo de la situación.

1. Elegir un modelo de IRT

Los modelos más comunes para ítems dicotómicos (correcto/incorrecto) son:

• 1PL (modelo Rasch). Asume que todos los ítems tienen la misma discriminación; solo se estiman la dificultad del ítem (b) y la habilidad (θ).
• Modelo 2PL. Estima tanto la dificultad (b) como la discriminación (a) para cada ítem, permitiendo que algunos ítems sean más informativos que otros.
• Modelo 3PL. Agrega el parámetro de adivinanza (c), que representa la probabilidad de responder correctamente al ítem únicamente por adivinanza (especialmente para ítems de opción múltiple).

Para escalas de calificación (por ejemplo, ítems de Likert), existen modelos de IRT politómicos, como el modelo de respuesta graduada o el modelo de crédito parcial, que extienden los mismos principios.

2. Estimación de parámetros del ítem

Dado un conjunto de datos de respuestas de encuestados:

• La IRT utiliza algoritmos (a menudo estimación de máxima verosimilitud o métodos bayesianos) para estimar a, b, c para cada ítem.
• Estas estimaciones expresan cuán probable es que los encuestados en diferentes niveles de habilidad respondan correctamente (o aprueben una categoría).

Este proceso generalmente requiere software especializado y a menudo se combina con pasos de análisis factorial para asegurar que la escala mida un solo rasgo dominante.

3. Estimación de habilidades de los encuestados (θ)

Una vez que se conocen los parámetros del ítem, el siguiente paso es estimar la habilidad de cada encuestado (θ):

• Para cada encuestado, el método de estimación encuentra el valor de θ que maximiza la verosimilitud de su patrón observado de respuestas.
• En pruebas adaptativas, θ se actualiza después de cada nueva respuesta al ítem, y el siguiente ítem se elige para ser el más informativo para la estimación actual.

Estos valores de θ pueden transformarse a escalas más familiares (por ejemplo, media 0 y SD 1, o escalas de 100 puntos), o vincularse a métricas externas como niveles de competencia.

4. Fórmulas del modelo

Para el modelo 2PL, la probabilidad P(θ) de que un encuestado con habilidad θ responda correctamente a un ítem (con parámetros a y b) es:

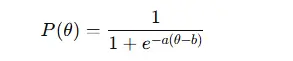
Para el modelo 3PL, que incluye la adivinanza (c):

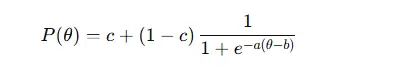
• a – discriminación del ítem
• b – dificultad del ítem
• c – parámetro de adivinanza
• θ – habilidad del encuestado

Estas funciones generan curvas características del ítem (ICCs) que muestran cómo cambia la probabilidad de una respuesta correcta con la habilidad.

5. Ejemplo (modelo 2PL)

Considera un ítem 2PL con:

• dificultad b=−1b = -1b=−1,
• discriminación a=1.5a = 1.5a=1.5,
• y un encuestado con habilidad θ=0.5.

La probabilidad de una respuesta correcta es:

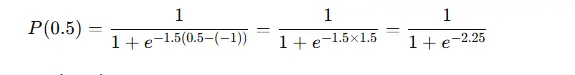
Numéricamente, esto es aproximadamente:

P(0.5) ≈ 0.905 (90.5%)

Así que para un encuestado en este nivel de habilidad, el ítem es relativamente fácil.

6. Usando salidas de IRT

Después de estimar los parámetros del ítem y de la persona, puedes:

• eliminar o revisar ítems malos (baja discriminación, ICCs extrañas),
• diseñar formas cortas que retengan la mayor parte de la información,
• construir pruebas adaptativas,
• comparar puntajes a través de diferentes versiones de una prueba,
• evaluar cambios en la habilidad a lo largo del tiempo (por ejemplo, pre-/post-entrenamiento en investigación experimental).

Las escalas basadas en IRT también pueden conectarse a otras métricas en tu sistema de medición, como CSI, ACSI, Compromiso de Empleados, o UEQ, para crear instrumentos más robustos y científicamente fundamentados.

En la práctica, implementar la IRT implica métodos estadísticos complejos y software dedicado, pero el beneficio es significativo: las pruebas y cuestionarios se vuelven más precisos, más justos y más comparables, especialmente cuando se utilizan repetidamente o entre diferentes grupos.