IRT: Análise de Itens de Teste

IRT (Teoria da Resposta ao Item) é uma família de modelos estatísticos usados para analisar dados de testes, questionários e pesquisas, onde cada item individual (pergunta) é importante.

Diferentemente da teoria clássica dos testes, que se concentra principalmente na pontuação total (soma de pontos entre os itens), a IRT modela a probabilidade de uma resposta específica a um item específico como uma função de:

• propriedades do item, e
• características (nível de habilidade ou traço) do respondente.

Os componentes-chave da IRT são:

• Dificuldade do item (b) – quão "difícil" é o item; itens com maior b são mais difíceis.
• Discriminação do item (a) – quão bem o item distingue entre respondentes com diferentes níveis do traço (por exemplo, habilidade matemática, ansiedade).
• Probabilidade de adivinhação (c) – em alguns modelos, a assíntota inferior que captura a chance de acertar um item por adivinhação (típico para questões de múltipla escolha).
• Habilidade do respondente (θ) – o traço ou habilidade subjacente que está sendo medido (por exemplo, proficiência em línguas, gravidade da depressão).

A IRT é amplamente utilizada em:

• educação (exames, testes de colocação, testes adaptativos computadorizados),
• psicologia e avaliação clínica (escalas para depressão, ansiedade, etc.),
• pesquisa social e de mercado (escalas de atitude, instrumentos baseados na Escala Likert, etc.),
• medição de UX e CX (por trás de alguns CSI, escalas estilo ACSI ou UEQ).

A IRT permite que você:

• entenda como cada item se comporta,
• construa testes adaptativos,
• equacione diferentes formas de teste,
• e acompanhe mudanças em habilidades ou traços ao longo do tempo (por exemplo, em estudos longitudinais).

Qual é o propósito da avaliação IRT?

A avaliação baseada em IRT é usada sempre que testes ou escalas precisam ser confiáveis, comparáveis e justas. As principais aplicações incluem:

1. Desenvolvimento e análise de testes

A IRT ajuda os designers de testes:

• avaliar a qualidade dos itens (dificuldade, discriminação, adivinhação),
• remover ou revisar itens com desempenho insatisfatório,
• garantir que um teste meça o construto pretendido de forma consistente.

Comparado a apenas olhar para porcentagens brutas ou pontuações totais, a análise baseada em IRT fornece uma visão muito mais rica de como cada item funciona em diferentes níveis de habilidade. Isso é crucial ao construir avaliações de alto risco ou escalas padronizadas (testes educacionais, pesquisas de engajamento de funcionários, instrumentos clínicos, etc.).

2. Testes adaptativos (CAT)

Um dos usos mais famosos da IRT é o Teste Adaptativo Computadorizado (CAT):

• O teste começa com itens de dificuldade média.
• Com base nas respostas do respondente, o sistema estima sua habilidade (θ).
• Os próximos itens são escolhidos dinamicamente para serem mais informativos para aquele nível estimado.

Isso proporciona:

• medição mais precisa,
• com menos itens,
• e redução do tempo de teste e fadiga.

Many large-scale exams and online assessment platforms rely on IRT-based CAT to deliver efficient, individualized testing.

3. Avaliação e comparação de itens e testes

Porque a IRT coloca tanto itens quanto respondentes na mesma escala latente (θ), ela permite:

• comparação de itens entre diferentes formas de teste,
• equação de testes (garantindo que as pontuações de diferentes versões sejam comparáveis),
• avaliação de como os itens se comportam em diferentes painéis, coortes ou culturas.

Isso é especialmente útil para programas longitudinais, exames de certificação regulares ou versões de teste multilíngues onde a justiça e a comparabilidade são importantes.

4. Pesquisa e desenvolvimento de programas educacionais

Na educação e treinamento, a IRT ajuda:

• analisar padrões de respostas corretas/incorretas,
• identificar áreas de conteúdo onde os aprendizes enfrentam dificuldades sistemáticas,
• refinar currículos e estratégias de ensino com base em insights a nível de item.

Quando combinada com pesquisa experimental e análise de séries temporais, a IRT apoia a avaliação rigorosa da eficácia do programa.

5. Avaliação transcultural e multilíngue

A IRT é poderosa em pesquisas transculturais:

• o mesmo teste pode ser administrado em diferentes idiomas,
• parâmetros de itens podem ser testados quanto à invariância (o item se comporta de maneira semelhante entre grupos?),
• itens problemáticos (tendenciosos ou específicos de cultura) podem ser detectados e revisados.

Isso ajuda a garantir testes justos e pontuações comparáveis entre países ou grupos demográficos, e muitas vezes anda de mãos dadas com revisões de especialistas do Método Delphi ou entrevistas cognitivas.

6. Diagnósticos e avaliação clínica

Na medicina e psicologia, a IRT apoia:

• a construção de escalas diagnósticas robustas (por exemplo, depressão, ansiedade, qualidade de vida),
• personalização de avaliações (formas curtas, versões adaptativas),
• acompanhamento do progresso do paciente ao longo do tempo com mais precisão.

Aqui, instrumentos baseados em IRT podem ser combinados com VAS, escalas Likert e outras ferramentas de medição, e analisados ao lado de métricas como CSI ou ACSI no trabalho de experiência do paciente.

7. Pesquisa social e psicológica

Nas ciências sociais e na pesquisa de mercado, a IRT é usada para analisar:

• atitudes e opiniões,
• traços de personalidade,
• escalas de comportamento (por exemplo, engajamento, satisfação, burnout através de ferramentas como MBI).

Ela complementa a análise fatorial e a análise qualitativa, e pode ser integrada em grandes painéis ou pesquisas transversais para melhorar a qualidade da medição.

Como é calculada a métrica IRT?

Na IRT, não existe "uma métrica", mas sim um modelo que descreve a relação entre:

• parâmetros do item (a, b, c), e
• habilidade do respondente (θ),

e a probabilidade de uma resposta dada (geralmente uma resposta correta ou endosse). Diferentes modelos de IRT são usados dependendo da situação.

1. Escolhendo um modelo IRT

Os modelos mais comuns para itens dicotômicos (certo/errado) são:

• 1PL (modelo Rasch). Assume que todos os itens têm a mesma discriminação; apenas a dificuldade do item (b) e a habilidade (θ) são estimadas.
• Modelo 2PL. Estima tanto a dificuldade (b) quanto a discriminação (a) para cada item, permitindo que alguns itens sejam mais informativos do que outros.
• Modelo 3PL. Adiciona o parâmetro de adivinhação (c), que representa a probabilidade de acertar o item apenas por adivinhação (especialmente para itens de múltipla escolha).

Para escalas de classificação (por exemplo, itens Likert), existem modelos IRT polytomous, como o modelo de resposta graduada ou modelo de crédito parcial, que estendem os mesmos princípios.

2. Estimando parâmetros do item

Dado um conjunto de dados das respostas dos respondentes:

• A IRT usa algoritmos (geralmente estimativa de máxima verossimilhança ou métodos bayesianos) para estimar a, b, c para cada item.
• Essas estimativas expressam quão propensos os respondentes em diferentes níveis de habilidade são a responder corretamente (ou endossar uma categoria).

Esse processo geralmente requer software especializado e é frequentemente combinado com etapas de análise fatorial para garantir que a escala meça um único traço dominante.

3. Estimando habilidades dos respondentes (θ)

Uma vez que os parâmetros do item são conhecidos, o próximo passo é estimar a habilidade de cada respondente (θ):

• Para cada respondente, o método de estimativa encontra o valor de θ que maximiza a verossimilhança de seu padrão observado de respostas.
• Em testes adaptativos, θ é atualizado após cada nova resposta de item, e o próximo item é escolhido para ser o mais informativo para a estimativa atual.

Esses valores de θ podem ser transformados em escalas mais familiares (por exemplo, média 0 e DP 1, ou escalas de 100 pontos), ou vinculados a métricas externas, como níveis de proficiência.

4. Fórmulas do modelo

Para o modelo 2PL, a probabilidade P(θ) de que um respondente com habilidade θ responda corretamente a um item (com parâmetros a e b) é:

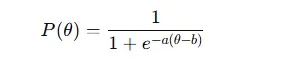
Para o modelo 3PL, que inclui adivinhação (c):

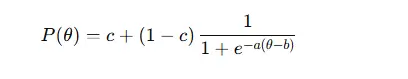
• a – discriminação do item
• b – dificuldade do item
• c – parâmetro de adivinhação
• θ – habilidade do respondente

Essas funções geram curvas características do item (ICCs) que mostram como a probabilidade de uma resposta correta muda com a habilidade.

5. Exemplo (modelo 2PL)

Considere um item 2PL com:

• dificuldade b=−1b = -1b=−1,
• discriminação a=1.5a = 1.5a=1.5,
• e um respondente com habilidade θ=0.5.

A probabilidade de uma resposta correta é:

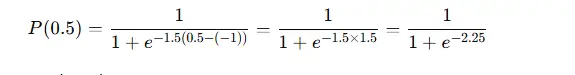
Numericamente, isso é aproximadamente:

P(0.5) ≈ 0.905 (90.5%)

Portanto, para um respondente nesse nível de habilidade, o item é relativamente fácil.

6. Usando saídas da IRT

Após estimar os parâmetros do item e da pessoa, você pode:

• remover ou revisar itens ruins (baixa discriminação, ICCs estranhas),
• desenhar formas curtas que retenham a maior parte da informação,
• construir testes adaptativos,
• comparar pontuações entre diferentes versões de um teste,
• avaliar mudanças na habilidade ao longo do tempo (por exemplo, pré/pós-treinamento em pesquisa experimental).

Escalas baseadas em IRT também podem ser conectadas a outras métricas em seu sistema de medição, como CSI, ACSI, Engajamento de Funcionários, ou UEQ, para criar instrumentos mais robustos e cientificamente fundamentados.

Na prática, implementar a IRT envolve métodos estatísticos complexos e software dedicado, mas o retorno é significativo: testes e questionários se tornam mais precisos, mais justos e mais comparáveis, especialmente quando usados repetidamente ou entre diferentes grupos.